| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 컴퓨터 구조
- 워게임
- 알고리즘
- 회귀 수식
- 리버싱 문제
- html
- 백준
- php
- C언어
- 웹
- 리액트
- 머신러닝
- writeup
- sql injection
- 해킹
- 리버싱 워게임
- 백준 알고리즘
- webhacking
- 웹해킹
- 리버싱
- CodeEngn
- 인공지능
- 리눅스
- webhacking.kr
- 보안
- 넘파이
- 자바스크립트
- MySQL
- 어셈블리어
- abex crackme
- Today
- Total
로보틱스 연구일지
[머신러닝] 로지스틱 회귀(Logistic Regression)으로 분류 실습 - 생선 종류 예측 본문
안녕하세요! 이번 시간에는 로지스틱 회귀를 이용하여 분류 문제를 풀어봅시다.
들어가기 앞서서 혹시 회귀가 뭔지, 로지스틱 회귀가 뭔지 헷갈리거나 들어는 봤지만 뭔지 정확히 모르겠다 하시는 아래 글을 참고해주세요:)
https://perconsi.tistory.com/82
[머신러닝] 회귀(Regression)의 종류(선형 회귀, 다항 회귀, 다중 회귀)와 시그모이드 함수의 역할
안녕하세요! 이번 시간에는 선형 회귀와 다항 회귀에 대해 알아봅시다. 선형 회귀와 다항 회귀에 대해 알아보기 전에 먼저 회귀가 전체 머신러닝 구조도 중에 어디에 있는지 알아봅시다. (저는
perconsi.tistory.com
또한 feature, target, label이란 단어에 익숙하지 않으시다면 아래 용어 정리 글도 보시고 오시는 걸 추천합니다.
이번 편은 위 글의 후속 편으로 다항 회귀의 실습을 통해 실제 사이킷런에서 어떻게 다항 회귀 식이 사용되는지 내부 방식을 뜯어보며 한 번 확인해 봅시다. 우리가 실제로 LogisticRegression이라는 함수를 사용할 때는 매우 간단하게
저는 개인적으로 이번 실습 하면서 알면 알수록 재밌다고 느꼈고 실제로 시그모이드 함수가 이런 역할을 하고 있다는 것이 너무 신기했습니다. 한 번 같이 봅시다.
로지스틱 회귀로 분류를?

위에서 말한 결론을 더 자세히 정리하면 위 식의 x 자리에 데이터의 feature가 각각 대응되어서 들어가면 클래스 내부에서 cost function을 이용해서 최적의 w(weight)와 b(bias)를 구해줍니다. 그러면 y값을 구할 수 있습니다. 그래서 이 y 값을 시그모이드 함수에 입력으로 넣어서 범위를 0에서 1 사이로 줄여주고 이를 0.5를 기준으로 "분류"를 할 수가 있습니다. (여기에서 이해되지 않으셔도 괜찮습니다. 아래 실습에서 조금 더 시각적으로 보여드리겠습니다)
1. 데이터분석
사용할 데이터는 혼자 공부하는 머신러닝+딥러닝에서 나온 생선 분류 문제입니다. 문제의 목표는 데이터의 특성을 보고 생선의 종류를 7개 중에 하나로 예측하는 분류 문제입니다.
우선 오늘 실습은 생선 데이터에 대해 아래와 같이 두 가지 방식으로 모델을 돌려볼 예정입니다.
- 로지스틱 회귀로 이진 분류 - 데이터를 이진 분류 문제로 바꾸어서 분류 실습
- 로지스틱 회귀로 다중 분류 - 원래 데이터 그대로 분류 실습
import pandas as pd
# 데이터 불러오기
fish=pd.read_csv('https://bit.ly/fish_csv_data')
fish
데이터를 불러왔으면 데이터 타입을 확인해 봐야겠죠?
# 칼럼의 종류 확인 - 칼럼은 타겟 칼럼 'Species'와 나머지 특성 칼럼 5개를 합쳐서 총 6개 존재
print(fish.columns)
print('columns number: ',len(fish.columns))[Output]
Index(['Species', 'Weight', 'Length', 'Diagonal', 'Height', 'Width'], dtype='object')
columns number: 6
그리고 이 칼럼 별로 데이터 타입을 확인해 봅시다. 이는 info() 메서드로 볼 수 있습니다. 타입을 보면 라벨(정답) 칼럼만
object로 문자열 칼럼이고 나머지 칼럼은 모두 실수로 이루어져 있네요. 별도의 전처리가 필요 없겠어요.
# 칼럼별 데이터 타입 확인 -
fish.info()[Output]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 159 entries, 0 to 158
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Species 159 non-null object
1 Weight 159 non-null float64
2 Length 159 non-null float64
3 Diagonal 159 non-null float64
4 Height 159 non-null float64
5 Width 159 non-null float64
dtypes: float64(5), object(1)
memory usage: 7.6+ KB
그럼 위와 같이 칼럼은 총 6개로 이루어져 있고 정답(label) 칼럼과 feature(특징) 칼럼 5개로 이루어져 있고 각 칼럼의 뜻은 아래와 같습니다.
| 칼럼명 | 뜻 | 데이터 타입 | 분류 |
| Species | 생선의 종 | object | label |
| Weight | 무게 | float64 | feature |
| Length | 길이 | float64 | feature |
| Diagonal | 대각선 | float64 | feature |
| Height | 키(세로 길이) | float64 | feature |
| Width | 너비(가로 길이) | float64 | feature |
저는 코드를 한국말로 뜻을 번역해서 이해하는 걸 좋아합니다.
정리하면 이 문제는 생선의 무게, 길이, 대각선, 키, 너비와 같은 특성을 고려해서 생선의 품종을 예측하는 문제네요.
간단합니다.
그리고 예측할 품종의 종류(label)를 알아봅시다. 생선의 종류는 아래와 같이 7종류가 있네요.
# 클래스인 Species 칼럼의 라벨 종류 확인
print(pd.unique(fish['Species']))[Output]
['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']문제는 feature를 보고 어떤 생선의 종류인지 맞추는 거였죠?
2. Train, Test 데이터 분리
그럼 이제 이 데이터의 feature(특성)과 label(정답)을 분리해 봅시다.
# feature(특성) 칼럼만 따로 분리
fish_input=fish[['Weight','Length','Diagonal','Height','Width']].to_numpy() # to_numpy()메서드를 추가한 이유는 모델의 입력 파라미터 형태로 넘파이를 요구하기 때문
# 타겟 칼럼을 모델에 정답으로 입력하기 위해 따로 분리
fish_target=fish['Species'].to_numpy()[Output]
# 데이터의 특성 칼럼을 상위 5개만 보기
print(fish_input[:5])
그럼 이제 더 세세하게 아래 네 가지 인자로 더 나눠줍니다.
- Train feature - 학습 데이터의 특성
- Train target - 학습 데이터의 정답
- Test feature - 테스트 데이터의 특성
- Test target - 테스트 데이터의 정답
# 훈련세트와 데이터 세트로 나눔
from sklearn.model_selection import train_test_split
train_input,test_input,train_target,test_target=train_test_split(fish_input,fish_target,random_state=42) # test_size 생략시 디폴트 값은 0.25
데이터를 나눠 주었으면 아래 StandardScaler로 전처리를 해줍니다. 여기서는 위에 나눠준 4가지 인자 중에 feature인 train_input과 test_input만 처리해주면 됩니다. 왜냐하면 아까 데이터 분석할 때 보았듯이 정답 칼럼은 문자열이고 feature는 실수여서 이 feature만 표준화해주면 됩니다.
# StandardScaler 클래스로 훈련 세트와 테스트 세트를 표준화 처리
from sklearn.preprocessing import StandardScaler
ss=StandardScaler() # 모델 객체에 할당
ss.fit(train_input) # 여기서 파라미터로 특성만 들어가는 이유는 숫자칼럼인 "특성만" 전처리하기 위함 (+data leackage 예방)
train_scaled=ss.transform(train_input) # test data의 input 표준화
test_scaled=ss.transform(test_input) # test data의 input도 마찬가지로 표준화해줌그럼 여기까지 모든 준비가 끝났습니다.
3. 이진 분류 문제로 바꾸어서 실습
원래 데이터는 7가지 중 하나를 예측하는 게 목표였는데 이진 분류로 바꾸기 위해서 우리는 임의로 정답 칼럼(Species) 중 클래스 값이 Bream(빙어)와 Smelt(도미)인 행만 골라내서 이진 분류 문제로 바꿔봅시다.
이렇게 이진 분류 문제로 먼저 바꾸어서 실습해보는 이유는 간단합니다. 작은 단위로 바꾸어서 보고 이해하면 더 큰 것을 이해하기 쉽기 때문에 먼저 이진 분류 문제로 실습해 봅시다.
이진 분류를 들어가기 전에 시그모이드 함수에 대해 간단하게 복습하면 시그모이드 함수는 불특정 한 범위의 입력값을 0에서 1 사이의 값으로 정규화해서 출력해준다고 했습니다.
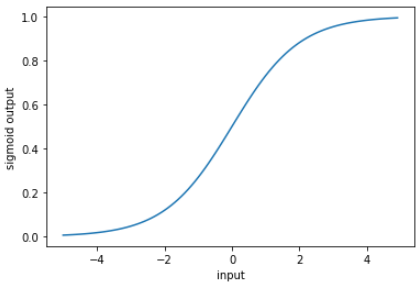
그럼 바로 이진 분류를 위해 라벨을 Bream(빙어)와 Smelt(도미)만 남겨봅시다.
이는 불리언 인덱싱을 통해서 할 수 있습니다. 불리언 인덱싱은 아래와 같이 True 값만 반환합니다.
# 불리언 인덱싱은 True인 위치의 값만 반환도 해줌
char_arr=np.array(['A','B','C','D','E'])
print(char_arr[[True, False, True, False, False]])[Output]
['A' 'C']
이를 이용하여 위에서 분리해서 전처리해주었던 학습 데이터의 feature와 target에서 라벨(정답)의 값이 빙어와 도미인 행만 남고 이를 feature와 target으로 나누어 주었어요.
- feature 데이터 프레임 - train_bream_smelt
- label 데이터 프레임 - target_bream_smelt
# 빙어(Bream)과 도미(Smelt)인 행만 select해서 feature와 target으로 할당
bream_smelt_indexes=(train_target=='Bream')|(train_target=='Smelt')
train_bream_smelt=train_scaled[bream_smelt_indexes]
target_bream_smelt=train_target[bream_smelt_indexes]
여기까지 하고 데이터 프레임을 자꾸 나누고 분리해서 헷갈리실까 봐 순서도를 준비했습니다.
보시면 초반에 전처리를 통해 파란색을 칠한 아래 4가지 인자가 나왔습니다.
- 학습 데이터의 특성 -> train_scaled
- 학습 데이터의 정답 -> train_target
- 테스트 데이터의 특성 -> test_scaled
- 테스트 데이터의 정답 -> test_target
그리고 방금 바로 위의 코드에서 이진 분류를 위해 라벨(정답)의 값이 Bream과 Smelt인 행만 남겨서 따로 떼준 데이터는 빨간색을 칠했습니다. 따라서 정리하면 파란색을 칠한 것은 라벨이 7개인 원본 데이터를 분리한 데이터 프레 임명이고
빨간색을 칠한 것은 이진 분류를 위해 분리한 데이터 프레 임명이에요.
그러니까 아래 순서도는 데이터를 학습시킬 데이터를 정리한 순서도예요.

3.1 모델에 학습 후 예측
그럼 여기까지 중간 흐름 정리를 했으니 계속 진행해 봅시다. 지금까지 이진 분류를 위해 데이터를 분리를 했습니다.
그러면 이제 한 번 모델에 돌려봅시다. LogisticRegression 알고리즘을 불러와서 학습(fit)시켜줍니다.
# 선형회귀 모델 import
from sklearn.linear_model import LogisticRegression
lr=LogisticRegression()
lr.fit(train_bream_smelt,target_bream_smelt)[Output]
LogisticRegression()
학습이 완료되었습니다. 그럼 이제 학습된 모델에서 클래스가 뭔지 확인해볼까요? 이는. classes_ 메서드로 확인할 수 있습니다. 클래스는 우리가 나눠준 대로 Bream과 Smelt가 들어가 있습니다. 여기서 유의할 점은. classes_를 호출하면 알파벳 순서대로 정렬된 클래스가 나오고 그 클래스는 각각 0, 1과 맵핑되어 있습니다.
(원래 문자열은 따로 인코딩 등의 방식으로 처리해줘야 하는데 모델이 해준 거예요)
# 이진 분류 모델의 클래스 보기
lr.classes_[Output]
array(['Bream', 'Smelt'], dtype=object)
계속 진행해봅시다. 그럼 지금부터 우리는 상위 5개의 데이터만 가지고 어떻게 모델이 동작하는지 정확하게 알아봅시다.
아래 코드는 모델에서 상위 5개의 데이터만 예측한 정답을 출력해주고 이는. predict(예측할 데이터)로 확인 가능합니다.
# 상위 5개의 예측 데이터 보기
print(lr.predict(train_bream_smelt[:5]))[Output]
['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
출력 결과를 보면 첫 번째 행의 데이터는 Bream이란 종으로 예측했고 두 번째는 Smelt 이렇게 차례로 상위 5개의 feature로 정답을 예측한 결과가 있습니다.
3.2 예측 과정 분석
그럼 이제 이게 어떻게 예측되었는지 보기 위해. predict_proba 메서드로 이 데이터들의 클래스별 확률을 봅시다.
# 클래스별 예측 확률
print(lr.classes_) # 차례로 0,1 클래스로 0이면 Bream, 1이면 Smelt
print(lr.predict_proba(train_bream_smelt[:5]))[Output]
['Bream' 'Smelt']
[[0.99759855 0.00240145]
[0.02735183 0.97264817]
[0.99486072 0.00513928]
[0.98584202 0.01415798]
[0.99767269 0.00232731]]
위의 출력 결과를 다시 보면 각 클래스의 확률이 0.5가 넘는 것은 Smelt로 0.5 이하는 Bream으로 예측한 것을 볼 수 있습니다. 물론 한 행의 합은 1이어야 하고요. 그런데 제가 방금 확률이라고 했죠? 어떻게 확률이 나오는지 한번 봅시다.

그러면 각 클래스별로 0.5를 기준으로 넘는 것으로 클래스를 예측하는 것은 알겠는데 이게 어떻게 구해지는지 봅시다.
포스팅을 시작할 때 LogisticRegression()은 이 다중 회귀 식과 시그모이드 함수를 이용해서 답을 구한다고 했죠? 한 번 봅시다.

우선 위 식을 다시 한 번 우리의 생선 분류 문제에 대입해 봅시다.
우리한테는 feature(특성) 칼럼이 5개 target(정답)이 하나 있었죠?
| 칼럼명 | 뜻 | 데이터 타입 | 분류 |
| Species | 생선의 종 | object | label |
| Weight | 무게 | float64 | feature |
| Length | 길이 | float64 | feature |
| Diagonal | 대각선 | float64 | feature |
| Height | 키(세로 길이) | float64 | feature |
| Width | 너비(가로 길이) | float64 | feature |
그럼 위식을 아래와 같이 바꿀 수 있습니다. 위 식에서 y는 예측하려는 정답이니 target이 되고 x는 각각 하나씩 feature 칼럼에 대응하니 아래와 같은 식이 나옵니다. 이해되시나요? 각각의 feature 칼럼인 Weight, Length, Diagonal, Height, Width가 각각 입력 자리인 x1, x2, x3, x4, x5에 들어가고 a, b, c, d, e는 이들의 가중치로 w1, w2, w3, w4, w5는 편의를 위해 a, b, c, d, e로 바꿨지만 이는 여전히 가중치이자 입력 값들의 계수입니다. 그리고 상수 f는 마찬가지로 편향입니다.
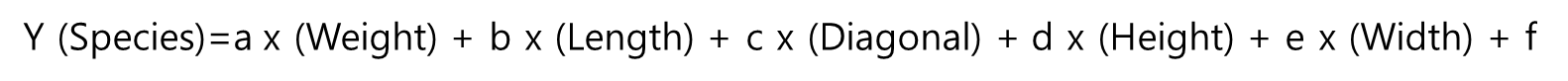
우리가 아까 train_bream_smelt [:5]로 상위 5개의 입력을 넣어줬죠? 그럼 위식에서는 결괏값이 y가 5개 나오게 됩니다.
이때 가중치(a, b, c, d, e)와 편향(f)은 로지스틱 함수에서 비용 함수를 통해 가장 최적의 값을 구해줍니다.
구한 가중치와 편향 값은 각각. coef_ 메서드,. intercept_ 메서드로 확인할 수 있습니다.
coef_와 intercept_ 속성에는 로지스틱 모델이 학습한 다중 회귀 방정식(선형 방정식)의 계수가 들어 있습니다.
# 로지스틱 회귀가 학습한 계수 확인 intercept는 계수
print(lr.coef_, lr.intercept_)[Output]
[[-0.4037798 -0.57620209 -0.66280298 -1.01290277 -0.73168947]] [-2.16155132]
위의 출력 값을 보시면 클래스 내에서 각각의 가중치와 편향을 잘 구한 것을 확인할 수 있어요.
그럼 위 수식은 다시 아래와 같이 바뀝니다. 이제 가중치 값과 편향 값 그리고 입력 x의 값까지 있으니 우리는 y를 구할 수 있겠네요.
(참고로 입력 값인 { weight, length, diagonal, height, width }는 5개의 데이터이므로 5개의 세트가 존재합니다.
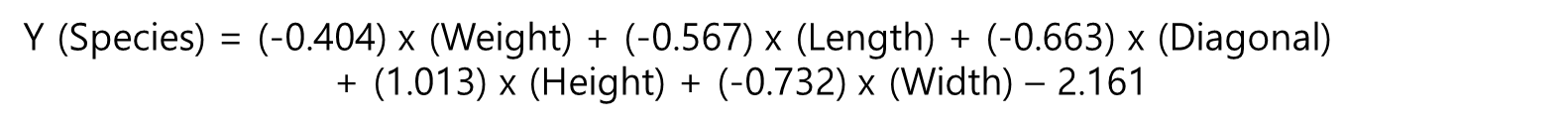
구한 Y 값은. decision_funsction으로 확인해볼 수 있습니다.
# z 값 출력, decision_function은 양성 클래스에 대한 확률 출력
decisions=lr.decision_function(train_bream_smelt[:5])
print(decisions)[-6.02927744 3.57123907 -5.26568906 -4.24321775 -6.0607117 ]성공적으로 값이 잘 나왔네요. 근데 이 값으로 어떻게 생선 종류를 예측하는 거죠? 값이 너무 범위가 다양하고 확률도 아니지 않나요? 이때 시그모이드 함수를 사용하면 값을 0에서 1 사이의 값으로 변환해주고 확률 값이 나옵니다.
즉 위 Y 값 5개를 시그모이드 함수에 통과시키면 확을 얻을 수 있습니다.
# 위 z 값을 시그모이드 함수에 출력 값을 0~1로 바꾸기
from scipy.special import expit
print(expit(decisions)) # expit가 시그모이드 함수[Output]
[0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]
위 코드를 보면 값이 너무 잘 나왔네요! 각각의 출력 값이 다중 회귀를 통해 y 값을 구하고 시그모이드 함수를 통과시켜서 확률을 구했습니다. 근데 뭔가 이상한 점이 있습니다. 우리가 아까 본 결과를 다시 봅시다. 위의 출력 값은 아래 predict_proba() 메서드의 출력의 두 번째 열의 값과 동일합니다.
즉 위의 decision_function은 양성 클래스(1, Smelt)에 대한 y 값을 반환합니다.
[Output]
['Bream' 'Smelt']
[[0.99759855 0.00240145]
[0.02735183 0.97264817]
[0.99486072 0.00513928]
[0.98584202 0.01415798]
[0.99767269 0.00232731]]그럼 여기까지 간단하게 어떻게 LogisticRegression() 클래스에서 예측이 이루어지는지 살펴보았습니다.
정리하면 다중 회귀 식을 이용해서 y 값을 구하고 그 값을 시그모이드 함수(또는 로지스틱 함수)를 통과시켜서 값의 범위를 줄여서 확률로 만들고 그 값을 통해 라벨을 예측했습니다.
회귀 식으로 y 값 구함 -> 시그모이드 함수 통과 -> 0.5 넘으면 해당 클래스 정답으로 예측
그럼 이제 이 원리를 이용해서 실제 다중회귀가 어떻게 이루어지는지 봅시다.
4. 로지스틱 회귀로 다중 분류
데이터는 아까 위의 순서도에서 파란색을 칠했던 나눠준 파일로 진행합니다.
우선 마찬가지로 LogisticRegression()를 사용해서 데이터를 학습해줍니다.
참고로 위 LogisticRegression()의 옵션 C와 Max_iter은 아래와 같이 정리할 수 있습니다.
| 파라미터 | 뜻 |
| C | 규제, 기본 값=1, 규제와 반비례로 C가 크면 규제를 줄이는 것 |
| Max_iter | 최대 반복 횟수, 기본값=100 |
단 위 실습과 다른 점은 이번엔 클래스가 더 늘어나서 시그모이드 함수 대신 소프트맥스 함수를 사용해서 값을 정규화해줍니다. 소프트맥스 함수는 시그모이드 함수와 동일하게 값을 0과 1 사이의 값으로 줄여주고 추가로 모든 입력의 값의 합이 1이 되도록 줄여줍니다.
4.1 모델 학습 후 성능 평가
아래 코드를 통해 규제를 줄여서 모델을 학습시키고 성능을 평가했습니다.
multi_lr=LogisticRegression(C=20,max_iter=1000)
multi_lr.fit(train_scaled, train_target)
# 학습데이터로 학습한 모델로 학습/테스트 데이터의 성능 평가
print(multi_lr.score(train_scaled,train_target))
print(multi_lr.score(test_scaled,test_target))[Output]
0.9327731092436975
0.925
성능이 아주 잘 나왔군요. 그래도 우리는 이게 어떻게 예측되는지 궁금하기 때문에 한 번 띁어봅시다.
4.2 예측 과정 분석
이진 분류 실습과 마찬가지로 상위 5개의 데이터의 예측 결과만 봅시다. 이번에는 종이 7개라 그런지 예측 결과도 다양하게 나왔네요. 아래 코드의 출력도 동일하게 첫 번째 인자는 첫 번째 데이터의 특성을 보고 예측한 정답이고 두 번째도 2번째 데이터의 특성을 보고 예측한 정답입니다. 즉 각각 데이터에 대한 예측 값입니다.
# 상위 5개 데이터만 분석
print(multi_lr.predict(test_scaled[:5]))[Output]
['Perch' 'Smelt' 'Pike' 'Roach' 'Perch']
그러면 5개 샘플에 대한 클래스별 예측 확률을 봅시다. 아까는 클래스가 두 개여서 칼럼이 2개였는데 이번에는 클래스가 7개여서 그런지 칼럼이 7개입니다.
# 5개 샘플에 대한 클래스 별 예측 확률
proba=multi_lr.predict_proba(test_scaled[:5])
print(multi_lr.classes_)
print(np.round(proba,decimals=3))[Output]
['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]
위 출력 결과에 대한 해석은 위와 동일하게 첫 번째 칼럼부터 7번째 칼럼은 각각 Bream, Parkki ~ 의 클래스에 차례로 대응되고 그에 대한 그 클래스에 대한 확률을 나타냅니다.
그리고 이 값은 소프트맥스 함수를 이용하여 나온 결과이기 때문에 한 행의 합은 1로 일치합니다. 또 이진 분류에서와 마찬가지로 한 행 중 가장 확률 값이 높은 클래스로 정답을 예측합니다. 그래서 첫 번째 행의 데이터도 3번째 칼럼의 값이 0.841로 가장 커서 3번째 칼럼인 Perch로 답을 예측합니다.

그리고 이젠 위 확률값이 나오는 과정을 보기 위해 먼저 회귀 식의 계수와 편향의 shape을 확인해봅시다.
# 다중 분류의 선형 방정식 shape 출력
print(multi_lr.coef_.shape,multi_lr.intercept_.shape) # 계수가 5개 세트인 행이 7개 존재, 절편도 7개[Output]
(7, 5) (7,)
그러면 위와 같이 이번엔 클래스가 7개여서 각각의 클래스별로 다른 가중치 값이 저장됩니다.
그리고 칼럼 5개에 대한 Weight 값이 저장된 행이 7개로 7세트 존재합니다. 즉 이진 분류를 할 때는 회귀식에 대한 Weight값 세트 하나로 값을 구했는데 클래스의 개수가 늘어나게 되면 식을 그 개수만큼 늘려서 동일한 원리로 답을 예측합니다. 다시 말하면 한 클래스별로 회귀 식을 구해서 예측합니다.
그럼 한 번 확인해 봅시다. 위에서 말한 대로 7개의 식에 대한 각각의 회귀 계수와 편향을 확인할 수 있습니다.
for i in range(7):
print(multi_lr.coef_[i], multi_lr.intercept_[i])[Output]
[-1.49002087 -1.02912886 2.59345551 7.70357682 -1.2007011 ] -0.09205178659877197
[ 0.19618235 -2.01068181 -3.77976834 6.50491489 -1.99482722] -0.26290885494521915
[ 3.56279745 6.34357182 -8.48971143 -5.75757348 3.79307308] 3.2510132723031
[-0.10458098 3.60319431 3.93067812 -3.61736674 -1.75069691] -0.14742956485584613
[-1.40061442 -6.07503434 5.25969314 -0.87220069 1.86043659] 2.654982827938869
[-1.38526214 1.49214574 1.39226167 -5.67734118 -4.40097523] -6.787829477252064
[ 0.62149861 -2.32406685 -0.90660867 1.71599038 3.6936908 ] 1.3842235834097936
그러면 또 위의 계수 별 가중치와 편향, 그리고 입력이 있으니 또 Y값을 구할 수 있겠네요.
마찬가지로 Y값은 decision_function을 통해 출력합니다.
# 소프트맥스 함수를 이용해서 확률로 바꿔주기, 각 칼럼이 식 1개에 대한 z 값
decision=multi_lr.decision_function(test_scaled[:5])
print(np.round(decision,decimals=2))[Output]
[[ -6.5 1.03 5.16 -2.73 3.34 0.33 -0.63]
[-10.86 1.93 4.77 -2.4 2.98 7.84 -4.26]
[ -4.34 -6.23 3.17 6.49 2.36 2.42 -3.87]
[ -0.68 0.45 2.65 -1.19 3.26 -5.75 1.26]
[ -6.4 -1.99 5.82 -0.11 3.5 -0.11 -0.71]]그러면 위 코드의 출력을 보면 한 행이 각각 하나의 데이터에 클래스별 대한 z값이 됩니다.
위의 이진 분류코드와 비교해서 봅시다. 보시면 아까는 y 값이 한 행으로 나왔고 각각의 칼럼이 한 샘플을 뜻했는데
여기서 클래스가 7개로 늘어나니 위의 출력에서 각각의 칼럼은 클래스별 확률이 되고 행은 샘플의 인덱스가 됩니다.

그러면 마지막으로 위 Y값을 소프트맥스 함수를 통해 범위를 맞추고 한 행의 합이 1이 되도록 해줍시다.
그러면 우리가 드디어 처음 다중 분류의 5개의 샘플에 대한 확률 값이 나오네요!
# 위 z값을 소프트맥스 함수로 확률로 바꿔주면 위 클래스의 예측 확률과 동일
from scipy.special import softmax
proba=softmax(decision,axis=1)
print(np.round(proba,decimals=3))[Output]
[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]그러면 지금까지 다중 분류할 때는 어떻게 예측이 이루어지는지 다중 회귀 수식과 소프트맥스 함수를 통해 살펴보았습니다. 이진 분류와 다중 분류의 차이점은 클래스별 회귀 수식의 개수 차이였지요? 어찌 됐든 결론은 한 클래스에 대한 확률을 구하는데 한 회귀식에 대한 파라미터를 구한다는 것을 기억해 주시면 감사합니다.
긴 실습 따라와 주셔서 감사하고 이해되지 않는 부분이나 수정할 부분이 있다면 댓글로 알려주세요.
읽어주셔서 감사합니다!
'인공지능 > 머신러닝' 카테고리의 다른 글
| [기계학습] 레이블의 분포도를 유지하여 데이터 분리와 교차검증 Stratified K-Fold,cross_val_score (0) | 2022.05.22 |
|---|---|
| [머신러닝] 회귀의 이해(선형 회귀, 다항 회귀, 다중 회귀)와 시그모이드 함수의 역할 (0) | 2022.05.06 |
| [머신러닝] fit(X,y)에서 변수 X,y의 의미와 지도학습의 흐름 및 머신러닝 용어정리 (data feature,data class) (2) | 2022.04.10 |
| [머신러닝] Numpy 기본 사용법 총 정리 (0) | 2021.10.08 |
| [머신러닝] AI 공부 방황기 겸 정리 (0) | 2021.08.23 |




